" /> 자료 구조론 5주차 - Stack과 연산자 | BlackWerf's Blog
포스트

자료 구조론 5주차 - Stack과 연산자

게시
By Junhyuk Son 6 분읽는 시간

수업 내용

선형 리스트

정의

  • 선형 리스트
    • 순서가 정해진 데이터 모임임
    • 예시) 요일 순서

표현 방법

  • Stack
  • Queue
  • 배열


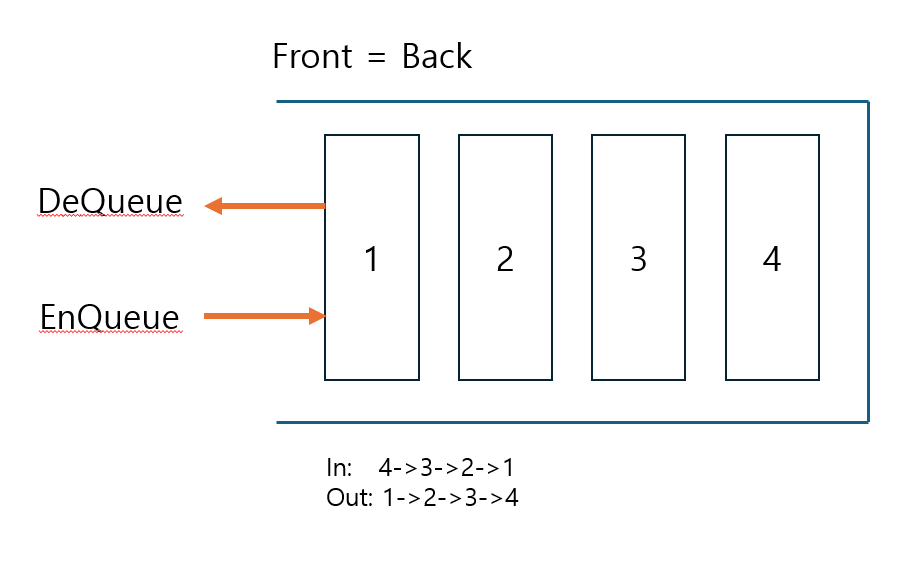
Stack

정의

  • 가장 최근에 삽입된 데이터가 먼저 삽입되는 방식의 메모리
    • L(ast)I(n)F(irst)O(ut) 혹은 Pushdown List라고도 불림
    • 데이터의 삽입과 삭제가 한쪽 끝에서 실행됨

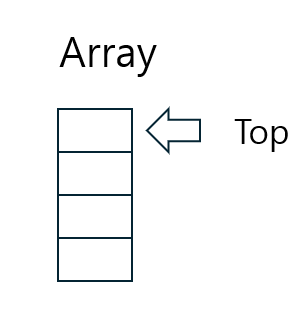
Image Alt 텍스트

Top Pointer

  • 위치 정보를 유지하기 위한 특수 레지스터
  • 가장 최근에 입력된 항목의 위치를 가지고 있음

구현 방법

길이를 알 경우

  • 1차원 배열을 사용함

    Image Alt 텍스트

길이를 모를 경우

  • Linked List를 이용해서 포인터로 구현함

    Image Alt 텍스트

관련 연산

Push

  • Stack에 데이터를 삽입함

  • 주의사항: overflow1

    를 주의해야함

Pop

  • 데이터에서 가장 마지막으로 입력된 데이터를 반환 및 삭제함

  • 주의사항: underflow2 를 주의해야함

Create
  • 하나의 공백 Stack S를 생성함
Top
  • S의 Top에 있는 항목을 결과로 반환함
Push(x, s)
  • S에 항목 x를 삽입 및 바뀐 스택의 결과를 반환함
Pop(s)
  • S의 Top 항목을 삭제 및 바뀐 스택의 결과를 결과로 반환
Empty(s)
  • S가 공백이면 true
  • S가 공백이 아니면 false를 반환함


  • 기본적인 연산은 Top Pointer를 증감하여 이루어짐

항목 여부 조사

초기 Stack 상태
  • 공백 상태로 설정됨
    • (s -> top) == 1
Stack의 공백 여부 조사
  • if문을 이용해 (s->top) == -1인지를 조사함

다중 Stack

  • 하나의 저장소 블록에 n개의 스택을 운영함
2개의 Stack을 운영
  • Stack1(top1, bottom1)
  • Stack2(top2, bottom2)
  • 2개의 Stacck에 Push연산을 집중 시 문제가 발생함
  • top1 = top2면 Stack Overflow가 발생함
N개 Stack 운영
  • 각 Stack은 top과 bottom 포인터를 포함하고 있음
  • Stack1의 empty 상태: top(i() = bottom(i)
  • Stacki의 overflow 상태: top(i) > bottom(i+1)


연산자 우선순위

  • 왼쪽 -> 오른쪽순서로 문자 단위로 연산이 진행됨
  • 컴퓨터에서의 연산자 순서는 일반적인 산술 계산을 위반함
  • 각 언어는 각 연산자별 연산 순서를 정의해놨으며, 우선순위가 높은 순서대로 진행됨
  • 다음은 연산자의 우선 순위이다
연산자 우선순위연산자 종류
1||
2&&
3<, <=, >, >=
4+, -
5*, /, %
6단항 연산자 -, !

우선순위가 동일한 연산자가 존재한 경우

  • 괄호 외: 가장 왼쪽 괄호부터 진행됨
  • 괄호 내: 우선순위가 같은 연산자가 중복 될 경우
    • 단항 연산자는 오른쪽에서 왼쪽 순서로 진행됨
    • 단항 연산자가 아닐 경우 왼쪽으로 오른쪽 순서로 진행됨

Polish 표현 방법

  • 산술식을 효율적으로 표기한 방법

    연산자 위치에 따른 분류
    • Infix(중위 표기법)
      • 피연산자 - 연산자 - 피연산자의 순서로 구성됨
        • Ex) A +B
    • Prefix(전위 표기법)
      • 연산자 - 피연산자 - 피연산자의 순서로 구성됨
        • Ex) +AB
    • Postfix(후위 표기법)
      • 피연산자 - 피연산자 - 연산자의 순서로 구성됨
        • EX) AB+
      • 컴퓨터 계산 방식임
        • 컴파일러에 의해 Infix표기가 Postfix 방식으로 변환됨
        • 스택을 이용해 수식 계산을 진행함
    Infix -> Postfix 변환
    • 연산자와 대응되는 오른쪽 괄호 바로 뒤 연산자를 이동 후, 괄호를 제거함
    Postfix의 장점
    • 괄호가 필요없음
    • 연산자의 순위가 필요없음
    • 스택을 이용해 식을 왼쪽->오른쪽 순서로 읽으며 쉽게 계산함
    Postfix 식의 스택을 이용한 계산
    • 수식을 계산하는 원소를 왼쪽에서 오른쪽 방향으로 읽음
    • 원소가 피연산자면 스택에 Push를 이용해 진행함
    • 원소가 피연산자가 아닐 경우, 필요한 수 만큼 피연산자를 스택에서 Pop하여 진행함
    • 이후, 연산 결과를 Stack에 Push함





  1. 스택의 영역부족으로 인해 항목이 저장 불가능한 현상으로, 배열 구조의 유한성으로 인해 발생함
    배열의 크기를 무한정으로 배정하면 메모리 활용성이 저하됨
    대안: 다중 스택 구조를 이용함 ↩

  2. ↩

학교 공부, 자료 구조론
23-2 자료구조론
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.