자료 구조론 6주차 - Queue와 리스트

수업 내용

Queue

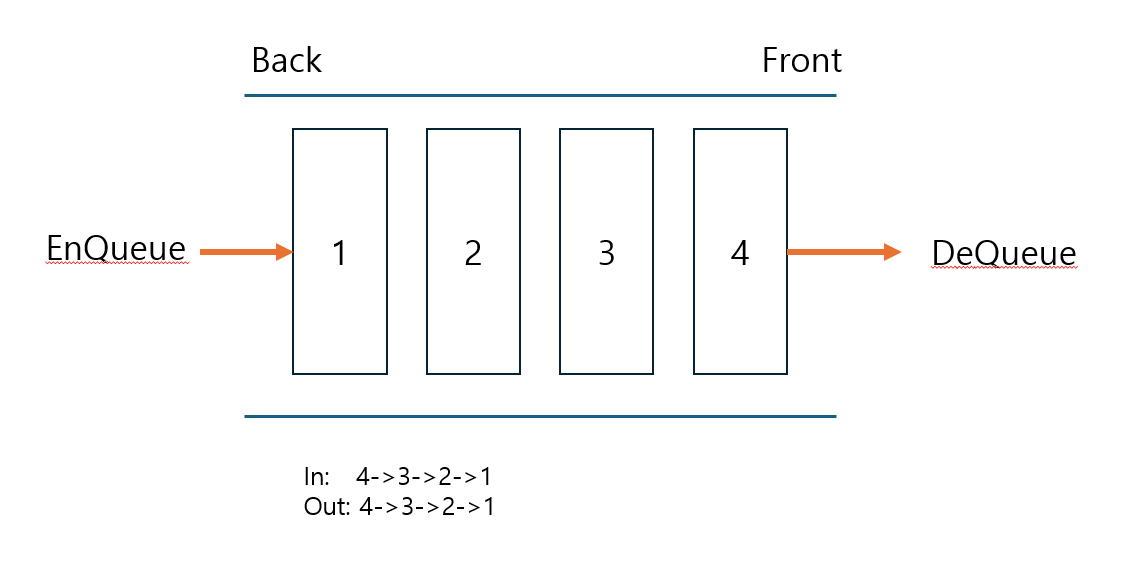
정의

• 한쪽에서는 항목이 삽입되고, 한쪽에서는 항목이 사라지는 형태의 구조의 메모리

• F(irst)I(n)F(irst)O(ut)

큐의 연산

• 대응하는 포인터의 값을 1+하여 연산을 진행함
  • 삽입: Front Pointer
  • 삭졔: Rear Pointer
• 논리적 삭제가 진행됨

구현 방법

• 배열
  • 1차원 배열로 구현
    • Q = [Q(0), …, Q(t-1)]
    • Front(Q): 큐의 Front Pointer가 지적하는 위치의 데이터
    • Rear(Q): 큐의 Rear Pointer가 지적하는 위치의 데이터
    • Noeal(Q): 큐에 있는 데이터 항목의 개수
• 연결 리스트

선언 방법

• 구조체를 이용해 선언함
• Queue는 3가지의 멤버가 포함 되어야함
  1. 항목을 보관하기 위한 유한 크기의 배열
  2. Front Pointer를 위한 정수형 변수
  3. Rear Pointer를 위한 정수형 변수

큐의 데이터 구조 응용을 위한 연산

• Create: 공백 Q 생성

• Insert(x,Q): 원소 x를 가르키는 Rear Pointer가 위치에 삽입 후, 새로운 큐를 반환함

  • 결과: rear(Insert(x, Q)) = s;
  • 삽입시 Overflow를 고려해야함

• Delete(Q): Front Pointer가 가르치는 위치 항목 삭제 이후, 새로운 큐를 반환함

  • 삭제 시 Underflow를 고려해야함
• Front(Q):큐의 Front 항목을 반환함

• Empty(Q): 큐가 비어있는지 여부를 반환한다

  • 큐가 비어있으면 True를 반환하다
  • 큐가 비어있지 않으면 false를 반환함

  
  

  • 큐에서의 항목 삽입/삭제 알고리즘은 시간 흐름에 따라 왼쪽에서 오른쪽 방향으로 이동함

  문제점

  1. Rear Pointer가 배열의 마지막 원소를 지칭하는 경우(q->r == n-1)

  • 반드시 큐에 n개의 항목을 지정해야 함

    불필요한 Overflow가 발생 할 수 있음

  • 이때 메모리 활용성이 저하됨

  불필요한 Overflow가 발생하는 경우

  Front Pointer > -1

  If(q->f) > -1, q=>queue0[], …, q->queue[q->f]는 사용 가능한 여유 공간임

  Full 상태의 Queue에서 연속적 항목을 삭제하는 경우

  -> Empty 상태인 Overflow가 발생함

해결 방법

큐의 항목들을 재배치

• 큐의 첫 항목인 q->queue[q->f+1]이 q->queue[0]에 위치하도록 큐 전체를 왼쪽으로 조정하기
• Front Pointer q->f의 값을 -1로 하고 q->r의 값을 조절하여 해결 가능함

문제점

• 재배치에 의한 연산이 필요함
  • 큐 안의 항목 수에 비례하는 처리 시간이 요구됨

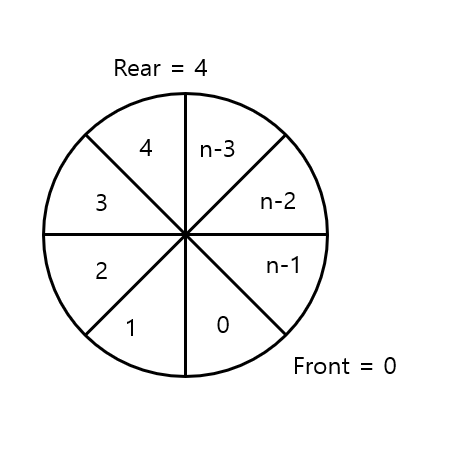
원형 Queue

• 큐의 배열을 선형 표현 대신 원형으로 표현한 Queue
• 배열의 첫과 끝이 연결된 형태
• 원형 Queue의 예시

원형 Queue의 연산

• 시계 방향으로 Front Pointer나 Rear Pointer를 1씩 증가 시킴

항목 삽입

• 새 Rear Pointer를 구하기 위해 나머지 모둘러 연산자를 이용함
  • 예시) rear = (rear+1) % n
• 주의 사항
  • (q->f) == (q->r)인 경우 Overflow가 발생할 수 있음

항목 삭제

• 새 Front Pointer를 계산해야 함

  • Modular 연산자를 이용해 구할 수 있음

    front = (front + 1) % n

• 주의 사항

  • (q->f) == (q->r)인 경우 Underflow가 발생 할 수 있음

큐의 응용

작업 스케줄링

CPU 스케줄링

디스크 스케줄링

• 우체국, 슈퍼 등 실생활에서 일괄 처리 작업을 진행 할 경우, 받아들여 진 순서대로 큐에 저장 후 순차 처리하는데,

  이 구조는 큐가 전체 성능에 많은 영향을 끼치므로 효율적으로 운영하는 것이 중요함

리스트

순서(선형) 리스트

정의

• 각 데이터를 연속된 메모리에 차례로 저장하는 리스트

• a(i)가 a(i+1)보다 선행하는 순서를 가지는 데이터들의 모음

  ​ 예시): 날짜 리스트

순차 사상

정의

• 순서 리스트를 배열로 구현할 때, 순서 리스트의 i번째 데이터가 배열의 i번째에 저장되는 상태

장점

• 메모리의 효율적인 사용이 가능함

단점

• 데이터의 삽입 및 삭제 발생 시, 리스트 내의 데이터를 순서 및 유지 시키는 작업이 필요함

데이터 삭제 시의 문제점

• n개의 데이터로 구성된 리스트에서, k번째 데이터의 삭제가 발생할 경우 데이터를 이동하는 횟수는 n-k회임

데이터 삽입 시의 문제점

• n개의 데이터로 구성된 리스트에서, k번째 데이터를 삽입할 때 데이터의 이동 횟수는 n-k+1회임

단순 연결 리스트

정의

• 논리적으로 연결한 데이터를 메모리에서 물리적으로 분산해 저장하는 비순차 사상 방법
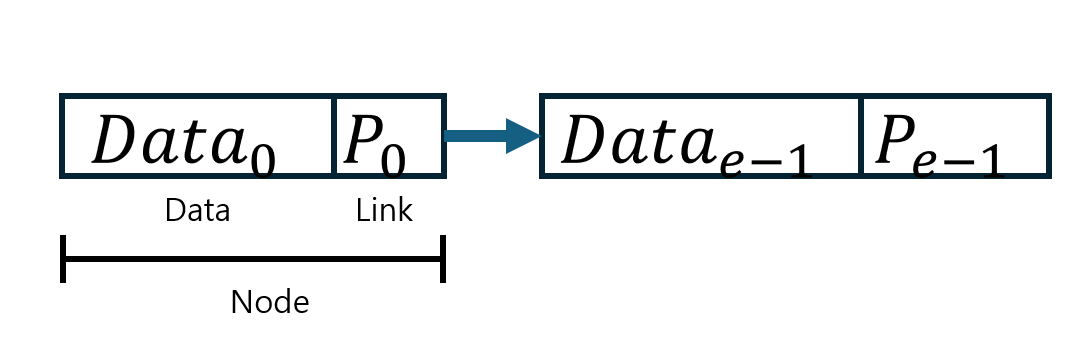
• 데이터들이 노드로 표현되며, 노드는 2개의 필드를 포함하고 있음

데이터 필드

• 다루는 데이터를 저장하는 역할

링크 필드

• 다음 노드의 주소나 위치 정보를 저장하는 역할

• 연결된 노드들의 집합으로, 링크 정보를 데이터 순서 유지하는데 사용됨

  • 마지막 노드의 링크 값: NULL

  

물리적 구조

• 데이터들이 기억장소 내에 차례대로 저장되지 않음
• 링크 필드 값으로 데이터 순서를 유지함