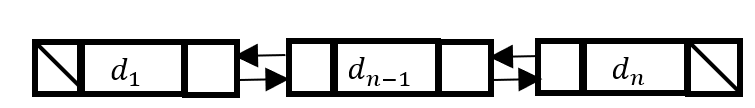자료 구조론 7주차 - 리스트와 그래프의 정의
리스트
원형 연결 리스트
정의
- 마지막 노드 링크 값이 Null이 아닌, 첫 번째 노드의 주소 값을 가짐
- 마지막 노드가 첫 번째 노드를 가르키도록 한 연결 리스트
이중 연결 리스트
정의
- 특정 노드에서 다음 노드 및 이전 노드까지 알 수 있도록 양방향이 순회 가능한 순서 리스트
노드 구조
- 3개의 필드를 가짐
논리 구조
이중 연결 리스트
이중 원형 리스트
왼쪽 끝 노드의 L링크 = 오른쪽 끝 R노드
오른쪽 끝 노드의 R링크 = 왼쪽 끝 L링
이중 원형 리스트에 원형 연결 리스트를 합친 형태임
리스트의 활용
다항식의 덧셈
단일 변수, 다 변수 다항식의 덧셈 연산에 적용 가능
\[p(x) = a_m * X^{e_m} + ...+ a_1x^{e_1}\] \[a_i = 계수, \qquad e_i = 지수\]예시
\[p(x) = 3^{14} + 2x^8 + 1\] \[+ q(x) = 8^{14} - 3^{10} + 10^6\] \[(p+q)x = (3+8)x^{14} - 3x^{10} + 2x^8 + 10x^6 + 1\]
그래프
Koenigsberg 다리 문제
- 하나의 다리에서 출발해 모든 다리를 경유해 출발점으로 돌아 올 수 있는지 결정하는 문제
그래프 사용 과정
각 지역
- 정점(Vertex)
모든 다리
- 간선(Edge)
- 오일러 그래프에서 고안해 문제를 해결함
정의
\[G = (V, E)\]- V(G): 하나 이상의 정점이나 노드들의 집합
- E(G): 2개의 정점 쌍으로 구성되는 간선들의 집합
- 두 집합은 모두 유한 집합임
분류
무방향 그래프
간선을 나타내는 정점 쌍에 순서가 없음
\[(V_1, V_2) = (V_2, V_1)\]
방향 그래프
화살표로 간선의 방향을 나타냄
방향 그래프에서는 정점 쌍에 나타난 정점 순서가 중요함
간선 표현 : \(<V_1, V_2>\)
\[V_1: 간선의 꼬리 \; V_2: 간선의 머리\] \[<V_1, V_2> \; \ne \; <V_2, V_1>\]
혼합 그래프(무방향 + 방향)
간선 개수에 의한 분류
- 다중 그래프
- 단순 그래프
종류
가중 그래프
- 각 간선에 가중 값이 있는 그래프
Multi Graph
- 두 정점 사이에 한 개 이상의 간선을 포함 함
- 다중 그래프의 다양성
- 하나의 간선에 할당된 가중 값
싱글 그래프
- 모든 2개의 정점 사이에 0개나 1개의 간선을 포함 함
널 그래프
- 독립된 정점들만을 보유함
- 간선들의 집합은 공집합
- 독립된 정점
- 어떠한 다른 정점들과도 연결되지 않은 정점
Colored Graph
- 몇 의 관계성을 구별하기 위해, 서로 다른 색이나 모양의 선을 사용하는 그래프
Complete Graph
- n개의 정점으로 구성된 무방향 그래프에서 간선 개수가 최대인 그래프
관련 단어
연결(Incident)
- 간선 \(e \in E\)가 정점의 쌍 \((V_1, V_2)\)인 상황에서 정점 \(V_1, V_2\)는 간선 e에 의해 연결
인접(Adjacent)
- 간선에 의해 연결된 두 정점은 인접함
Path
- 임의의 정점에서 다른 정점에 이르는 일
- 임의 간선의 머리가 다음 간선의 꼬리가 되는 간선들의 열
Length
- 경로 상 간선들의 개수
Simple Path
- 하나의 경로 상에 있는 모든 정점들이 서로 다름
기본 경로(Elemantary Path)
- 하나의 경로 상에 있는 모든 간선들이 서로 다름
Cycle
- 출발점, 도착점이 같은 단순 경로
Cyclic Graph
- 사이클이 존재하는 그래프
진입 차수(Indegree)
- 주어진 정점으로 향한 간선의 개수
전출 차수(Outdegree)
- 주어진 정점에서 시작한 간선의 개수
전체 차수(Total Degree)
- 정점에서의 진입 차수와 전출 차수의 합
Loop
- 간선의 시작점과 끝점이 같은 정점
- 길이가 1인 경로임
부분 그래프(Sub Graph)
- 그래프 G의 정점 및 간선의 부분집합으로 구성된 그래프
비사이클 그래프(Acyclic Graph)
- 사이클이 존재하지 않은 그래프
Dag(Directed Acycic Graph)
- 방향이 있는 비사이클 그래프
Connected
- 무방향 그래프 G에서 정점 \(V_p \rightarrow V_q\)까지의 경로가 있으면 \(V_p, V_q\)는 서로 연결됨
Connected Graph
- 임의의 정점 \(V_p, V_q\)가 연결되었을 때의 그래프
표현 방법
인접 행렬
가정
- 그래프 G = (V, E)가 n개의 정점을 포함함
인접 행렬
- nxn의 2차원 배열
- 배열의 구성요소 a
- 행과 열의 개수가 같은 정방 행렬
- 모든 요소가 0이나 1로 구성됨
- 인접행렬을 통해서 임의의 두 정점 i와 j를 연결하는 간선의 존재 여부를 쉽게 결정 가능함
- i번째 행에서 값이 1인 원소의 수 = 정점 \(V_i\)의 진출 차수
인접 리스트
인접 행렬의 n개의 행을 n개의 연결리스트로 표현함
그래프의 각 정점에 하나의 연결리스트가 존재함
리스트 i에서의 각 노드들
- 정점 i에서 인접된 정점들
각 노드는 2개의 필드를 포함하고 있음
1) 정점 필드: 해당 정점의 인덱스 2) 링크 필드: 다음의 인접된 정점
- 한 정점의 진출 차수
- 대응되는 인접 리스트의 노드 수
- 정점의 진입 차수
- 역 인접 리스트나 직교 리스트를 이용함
역 인접 리스트
- 특정 정점으로 진입하는 모든 인접 정점에 대한 노드들로 구성됨
- 진입 차수의 계산을 위해 노드로 들어가는 간선에 대해 인접 리스트의 형태를 구성함
- 인접 행렬에서의 각 열에 대한 연결 리스트
인접 다중 리스트
- 다중성의 정도나 가중값: \(W_{ij}\)
- 각 원소의 a값:
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.